[8/11/2024] - math for gamedev

hello! today i'll be explaining some math stuff you can (and probably will) use when making games. this is supposed to be a simple guide for beginners
this list doesn't cover all that is used in gamedev, i've included only a few topics i have already used before and i find essential to know
most of them is basic math but i think it would be beneficial to list them anyways

table of contents

• binary operations
• measuring distance
• dealing with angles

binary operations

boolean values (aka values that can only be true or false) _{aka bit} are the most basic unit of a computer. knowing how to manipulate them means to know how to use a computer. and you manipulate them using what nerds call bitwise operations. these are the most basic operations you can do on a computer

the operations i'll be covering here are not all of the existing operations but only the ones i find essential yeah i said this before i think

and

the and operation (usually represented with a &) returns 1 (true) if all of the inputs are also 1.
you can think of it like this: if input-a is true and input-b is also true, then return true.

however, this operation, like all of the others, can be applied to multiple bits at once. like this:

a: 0 0 1 1 &
b: 0 1 0 1 =
o: 0 0 0 1

each binary place is and-ed with all of the bits in the same binary place. similar to how you would do with addition, if you decide to write it vertically.

using this we can create what we call a mask. a mask is a collection of bits which indicate which bits contain important data.
here's an example

lets say, hypothetically, you have secret agents in a video game. okay, lets even say, you want to describe their permissions. right so, in this scenario, there are three non-exclusive categories of permissions: read documents, write to those documents and execute the orders in those documents.
you could describe each permission as a bit in a string of bits.

perms: r w x
- oak: 1 1 0
- red: 1 0 0
- ash: 0 1 1

and if you want to check if each agent has a certain set of permissions, you can & them with another set of bits with the desired permissions.

perms: r w x
- oak: 1 1 0 &
- msk: 1 0 1 =
- out: 1 0 0

the output shows that from the permissions we wanted (the mask) only the read permission is available.

however, we might want to add more permissions, or check if a single one of the permissions are available. for this, we will need a new operation.

or

the or operation (usually represented with a |) returns 1 if any of the inputs are 1.
so, if input-a is true or if input-b is true, return true.

this operation can also be used on multiple bits at once.

a: 0 0 1 1 |
b: 0 1 0 1 =
o: 0 1 1 1

if we want to add a permission to someone, we can create a mask with only the new permissions set to true and we | them with our current permissions.

perms: r w x
- red: 1 0 0 |
- msk: 1 0 1 =
- out: 1 0 1

the output is the permissions that red had, plus the permissions we wrote on the mask. since red already had the read permission, it is the same on the output. the output also has the execute permission, which came from the mask we wrote.

to check if a single permission is enabled we create a mask containing this single permission, do | in our permissions and the mask and then check if the original permissions are equal to the result.

perms: r w x
- red: 1 0 0 |
- msk: 1 0 0 =
- out: 1 0 0 // here the permissions match, so the output is the same.

perms: r w x
- ash: 0 1 1 |
- msk: 1 0 0 =
- out: 1 1 1 // output is different from the permissions, so we don't have at least one of the permissions of the mask.

this is really great and all but what if we want to set a single permission to false? what if we want to toggle our permissions?
again, this can only be achieved with the help of another operation.

xor

the xor operation is really powerful. its name stands for exclusive or. it might be unintuitive for beginners, but it is really simple actually. the xor operation returns 1 if the inputs are different and 0 if they are equal. you can think of it as: if input-a is true or input-b is true, but not both, return true.

here is the truth table:

a: 0 0 1 1 ^
b: 0 1 0 1 =
o: 0 1 1 0

so if we want to toggle one of the permissions we just need to set a 1 in our mask

perms: r w x
- red: 1 0 0 ^
- msk: 0 0 1 =
- out: 1 0 1

and to set just a single one of the permissions to false, we use & on our mask and the input, and ^ this output with the original permissions

perms: r w x
- oak: 1 1 0 &
- msk: 0 1 1 =
- out: 0 1 0

- oak: 1 1 0 ^
- out: 0 1 0 =
- out: 1 0 0 // notice the execute flag is still set to false!

i think this is all you will need for game development. maybe you will need to learn more if you dive deeper if i would guess, you would be doing weird shader optimizations but in any case, a good resource i found to learn more about these operations is nandgame! nandgame is composed of a series of small exercises which introduce you to the lowest level you can reach in a computer. it teaches about all of these binary operations and their implementations in actual hardware. the game is more focused on how computers are made but i think it will greatly help you understand this part of computers

measuring distance

this one is really simple.
most engines and frameworks have an implementation of a distance function, where you input two points in space as vectors and get a floating point number representing the distance between them.
for this guide, i'm going to explain how you can write your own distance function.

basically, we use the pythagorean theorem to calculate the distance.

if you saw this in school before, you probably know that the pythagorean theorem is used to measure the lengths of the edges of a right triangle.

first, we need to build the triangle. we start with our two positions.



since we want the distance between the points, we can trace a line using our two points. this line represents the distance between point a and point b. we will call the line d for distance.

we can make a right triangle out of this. we just need to align a new point to the two other points



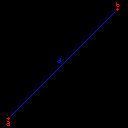
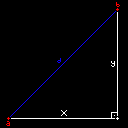
now this is looking great. we could apply the pythagorean theorem with this. however we still need to calculate the x and y values. to calculate them, we need to know where the white point is located. luckily, since we use the a and b points to create it, and we know there is a perfect 90 degree angle or a .5πrad angle, if you use the superior metric we can infer that the position of the white point is equal to the x position of the b point and the y position of the a point.



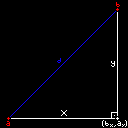
and to calculate the distance of the x and y lines we can use the x position of b subtracted by the x position of a and do the same for the y line, but using their y value.



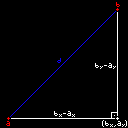
now we can finally use the pythagorean theorem!

the definition of the pythagorean theorem is the following:
a² + b² = c²
where a and b are the sides of the triangle with the 90deg angle or the legs of the triangle , and c is the larger side or the hypotenuse. using our drawing as reference, we can see that a is equal to b_x - a_x, b is equal to b_y - a_y and c is equal to our distance.

replacing these in our equation we get this:
(b_x - a_x)² + (b_y - a_y)² = d²

and to isolate d we take the square root of both sides of the equation, which would become this:
√((b_x - a_x)² + (b_y - a_y)²) = d

now we can write our own distance function! i'm going to write it in python, but it should be easy to replicate it in another language. here is the code:

import math
# defines a point
class Point:
 def __init__(self, x, y):
  self.x = x
  self.y = y

# the function resolves the equation we found earlier
def distance(point0, point1):
 a = point1.x - point0.x
 b = point1.y - point0.y
 sum = a * a + b * b
 return math.sqrt(sum)

def __init__():
 first_position = Point(1, 3) # creates a point at (1, 3)
 second_position = Point(4, 7) # creates a point at (4, 7)
 points_distance = distance(first_position, second_position) # calculates the distance
 print(points_distance) # should print 5.0

the distance function takes two points as arguments, where each point has two properties: a x value and a y value. we then calculate the a in the pythagorean theorem, then the b, we get the sum of the two and then we take the square root. we are done with it!

however, this is only for 2d space. what about 3d space?

we need to extend our vectors to include the 3rd dimension and also upgrade the pythagorean theorem

so our vectors become (x, y, z) and we can expand the pythagorean theorem like this:
√(a² + b²)² + c² = d²

notice we changed one of the letters to put another pythagorean theorem in place

we can simplify this to:
a² + b² + c² = d²

and now we can input our distances
√((b_x - a_x)² + (b_y - a_y)² + (b_z - a_z)²) = d

the 3d version of the code is this:

import math
# defines a point
class Point:
 def __init__(self, x, y, z):
  self.x = x
  self.y = y
  self.z = z

# the function resolves the equation we found earlier
def distance(point0, point1):
 a = point1.x - point0.x
 b = point1.y - point0.y
 c = point1.z - point0.z
 sum = a * a + b * b + c * c
 return math.sqrt(sum)

def __init__():
 first_position = Point(1, 3, 1) # creates a point at (1, 3, 1)
 second_position = Point(4, 7, 1) # creates a point at (4, 7, 1)
 points_distance = distance(first_position, second_position) # calculates the distance
 print(points_distance) # should also print 5.0

ok, this is all for distances. we could go further with 4 dimensions but most people don't make games in 4d. i wonder why

dealing with angles

sometimes you want to get the angle between two objects or get the position of something based on an angle. the process is simple but it could be quite confusing if you don't understand the math behind it. also, knowing your ways with trigonometry is fundamental to game development. specially for 3d games. so this part will be dedicated to the basics of trigonometry

there are two main functions we need to understand: the sine and cosine functions. these work as the base for all of trigonometry. they are used to convert an angle into a number between 0 and 1. however, understanding how they do it is fundamental to knowing how to efficiently use them.

i think the best explanation is with pictures.

first, think on the cartesian plane



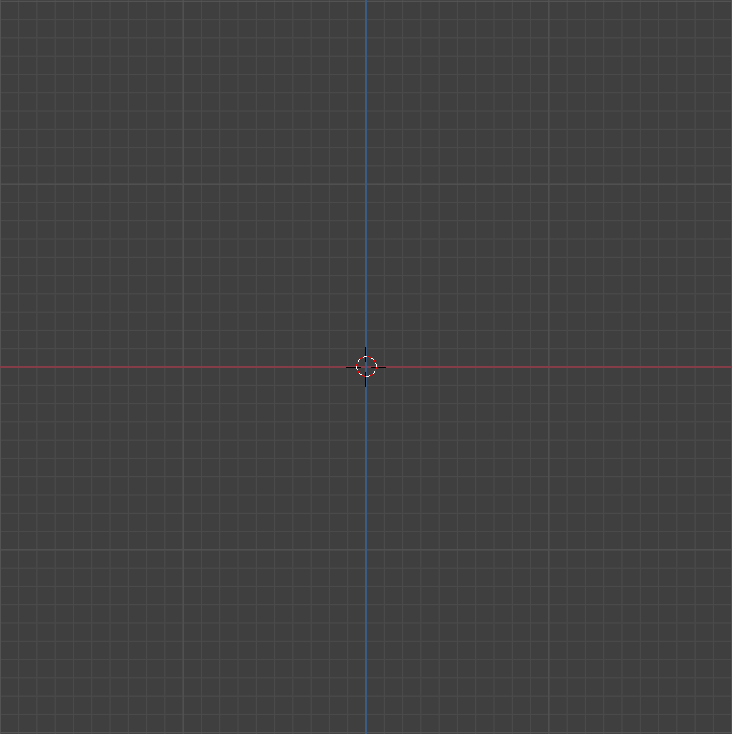
this is a representation of 2d space. going right will increase your x position and going left will decrease. going up will increase your y position and going down will decrease.
now we add a circle.



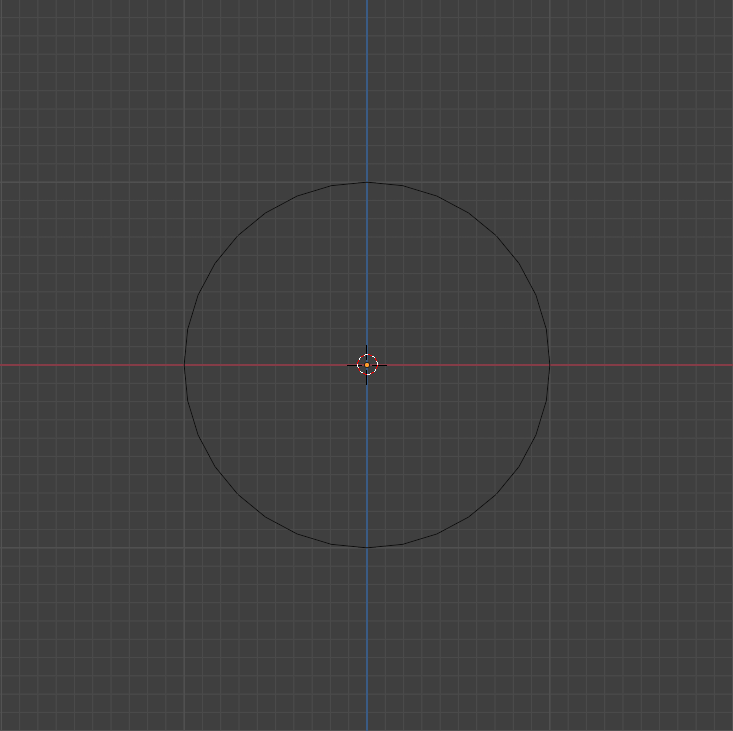
this circle has a radius of 1, which means the distance of any point from the circle to its center will have exactly 1 unit of length.

we will choose a random angle from the circle. i will choose 64° because i like this number it is a power of 2

now we mark a point on the circle which marks this angle



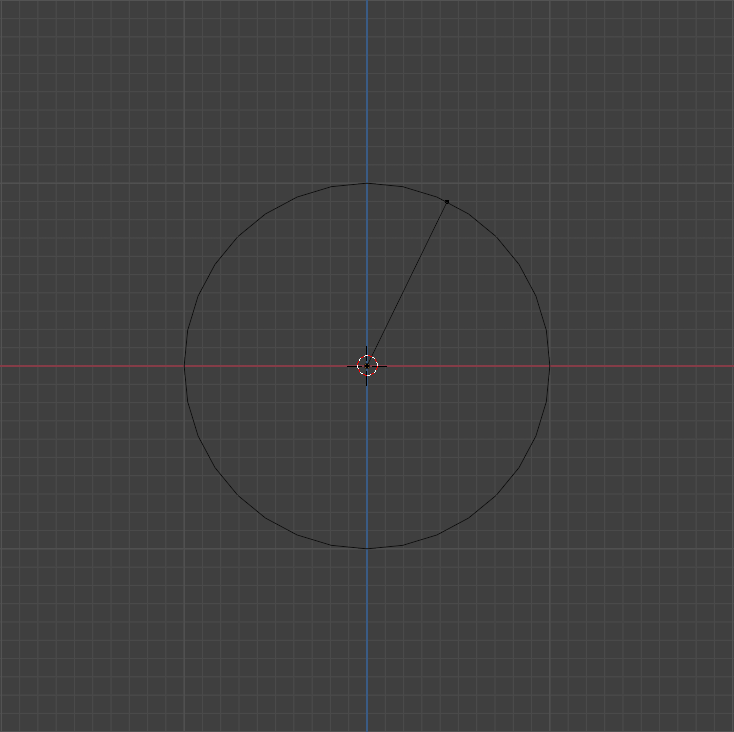
note that we start counting the angle from the east and go counter-clockwise
okay: now the fun part. how do we calculate the x and y position of the point we just marked?
this is where the sine and cosine functions enter. they return the x and y position of a point in a circle, based on an angle.
so if we try and calculate the sin(angle) and cos(angle), we should be able to get the position!

if we put this in a calculator, we get the following:



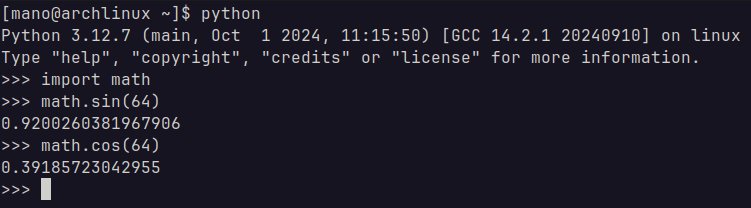
0.92 for the vertical position (sine is the vertical position) and 0.39 for the horizontal position
so if we check the position of the point we get...



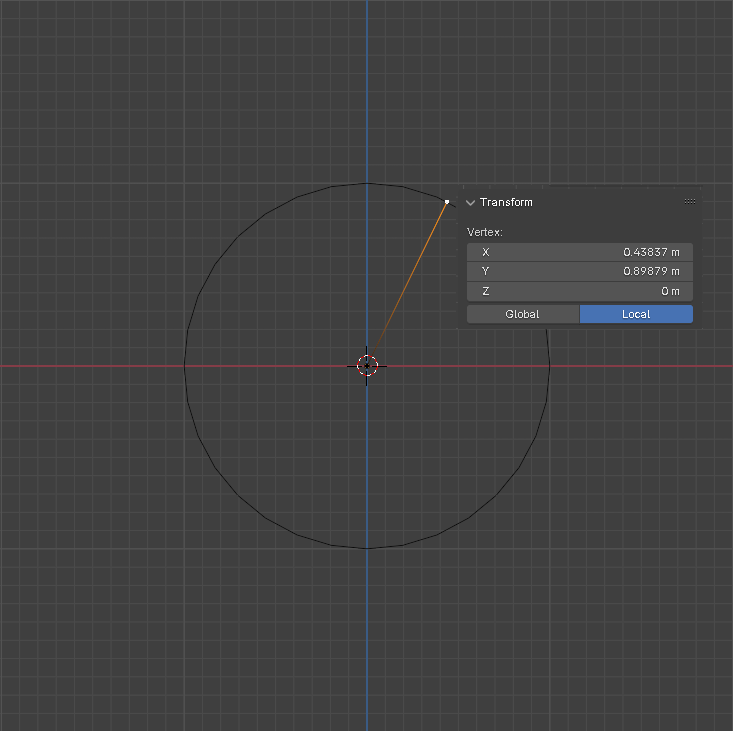
...a completely different result??

how can this be possible??

if we look at the documentation for the sin() function we can see an interesting detail:



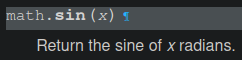
"x radians". what is that?
we know x is our angle, but what does radians mean?

radian is an alternative metric to represent angles. kinda like what fahrenheit is to kelvin
radians are based on the ratio of the circumference of the circle and its diameter. in other words, radians are based on π!

in radians, half a circle is equivalent to the number π. knowing half a circle is equivalent to 180°, we can use cross-multiplication and simply divide π by 180 and then multiply the result by our angle! or we could use the radians() function in python but that is the boring way of doing it

if we do that we get 1.12rad, but i prefer leaving the multiplication by pi explicit to facilitate reading, which would be 0.36πrad.
now, if we go back to the sine and cosine functions and plug this new number we get the following:



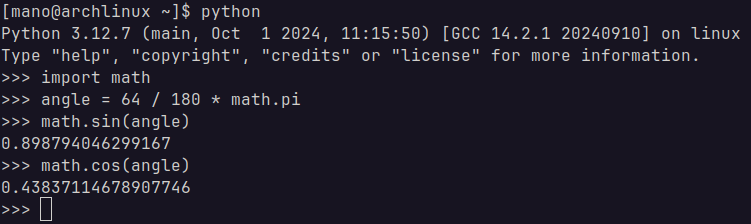
we get 0.90 for the vertical position and 0.44 for the horizontal position. this matches the point position!

so, if you want to get the position of something based on an angle, you just need the angle in degrees and calculate the vector (cos(a), sin(a)). and in the case you need a radius bigger or smaller than 1 unit, you multiply the vector by the desired radius.

ok, but there is still something missing. how can we get the angle between two points?

we need the inverse functions of sine not to be confused with the inverse or reciprocal of sine, which would be 1/sin(x) and cosine. that would be the arcsine and arccosine functions. these functions take a number from 0 to 1 and return the angle in which their inverse would return this number. and of course, the angle returned is usually in radians, but it is better to look at the documentation just to be sure.

if we use the position we got previously, we get these results:



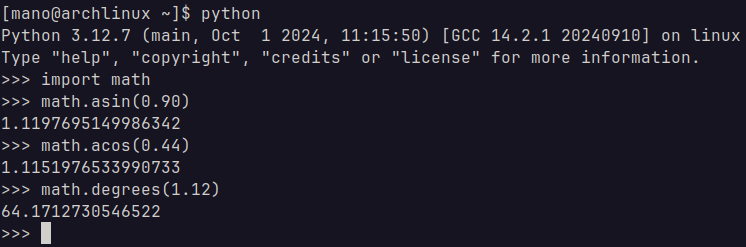
there is a little bit of imprecision due to me rounding the numbers but it is very clear that we got 0.36πrad back!

now you can apply these however you want :)

note that for the arcsine and arccosine functions you need to divide the position by the radius of the circle. usually the radius is the distance between two points

i think this concludes this segment.